Picscoreの原理
Picscoreによる解析の根幹となる「フラクタル」とは
フラクタル(Fractal)はMandelbrot(1975)によって提唱された概念で、無限の繰り返しパターンを持つ自己相似な形状、現象を意味します。
- 語源はラテン語「fractus」から「不規則に壊れてバラバラとなった状態、断片」という意味です。
- 自然界のランダムな複雑さ、空間パターンの様子を表す特徴量として用いられています。
- 絵画や風景などの視覚情報のフラクタルがその好感度と関連があることが多くの研究で主張されています。
(Taylor, Micolich, & Jonas, 1999; Akks & Sprott, 1996; Pickover, 1995; Taylor, 2001; Taylor, Spehar, Clifford, Newell, & Martin, 2005; Hagerhall, Purcell, & Taylor, 2004; Cooper & Oskrochi, 2008)
自己相似とは
ある図形の断片を取ってきたとき、それより小さな断片の形状と図形全体の形状とが相似である場合を指します。「自分自身の中に自分がある」、「局部を拡大しても同じ構造がある」という状態のことです。
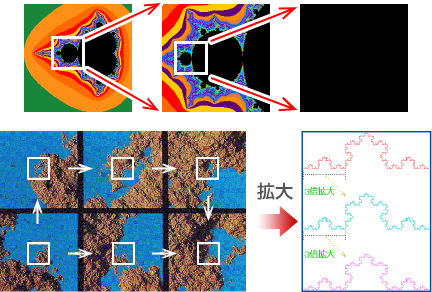
さまざまなフラクタルの例
-
自然界のフラクタル

-
人工的なフラクタル

複雑さの程度を表す尺度「フラクタル次元」とは
- フラクタル次元はフラクタルの自己相似の特徴量を定量化した指標で、複雑さの程度を表す尺度として使用されます。
- フラクタル次元は非整数値で、図形などが複雑であればあるほど値が大きくなります。
フラクタル次元の算出例
自己相似性のある図形において、図形を1/n に縮小した相似形m個によって構成されるとき、フラクタル次元(相似性次元):
D= log(m)/log(n)
log(元の図形と相似な同じ図形の数)/log(等分割した数)
- 例)コッホ曲線
- ➊線分を引く。
- ➋線分を3等分し、中央の線分を1辺とする正三角形を描き、下の辺を消す。
- ➌得られた4つの線分に対して同じ操作を繰り返し、元の図形と相似な同じ図形を作成する。
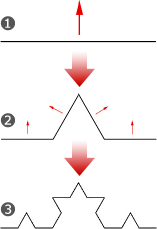
D = log(m)/log(n) = log(4)/log(3) = 1.2618
フラクタル次元と複雑さの関係
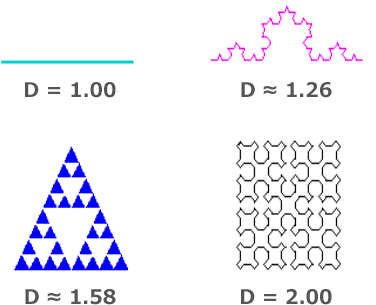
以下に、各図形のフラクタル次数を示します。
図形が複雑であればあるほど数値が高いことが分かります。
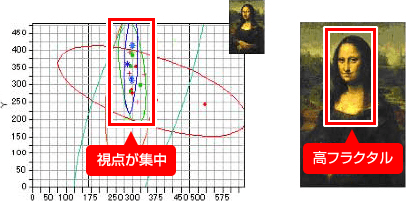
ヒトの視線の集中位置とフラクタル次元の高い位置が一致
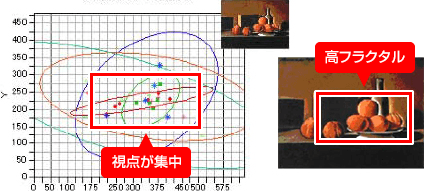
- 6つの絵画を対象に、アイカメラを使用して視点の集中位置とフラクタル次元との関係を調べました。
- その結果、フラクタル次数が高い箇所に視点が集中する傾向がみられました。
Relationship between image gaze location and fractal dimension:Masayushi Nagai, Mayumi Oyama-Higa, ; Teijun Miao,Systems, Man and Cybernetics, 2007. ISIC. IEEE International Conference on

① Leonardo da Vinci
② Alphonse Maria Mucha
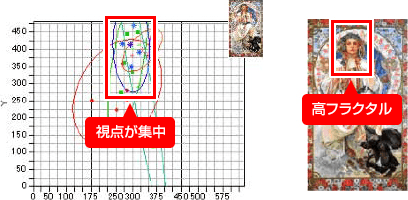
③ Johannes Vermeer
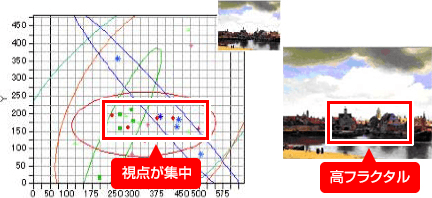
④ Jean-Baptiste Camille Corot
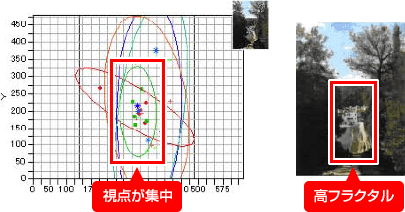
⑤ Francois Boucher
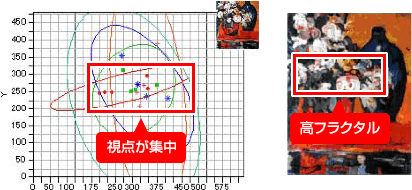
⑥ Giorgio Morandi
曼荼羅のフラクタル次元は最高点
- 曼荼羅(まんだら)とは、仏教(特に密教)において聖域、仏の悟りの境地、世界観などを仏像、シンボル、文字、神々などを用いて視覚的・象徴的に表したものです。
- 曼荼羅模様は、フラクタル次数が非常に高いことで知られています。特に中心部がフラクタル次数が高くなっております。
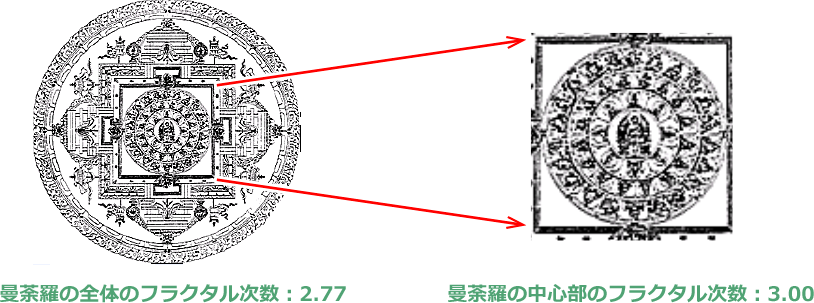
※フラクタル次数は、2.0〜3.0の小数点のついた値で、フラクタル次元が高いほど3.0に近づきます。
缶ビールのパッケージ・デザインとフラクタル次元の関係
- 45種類の缶ビール(地ビール)のパッケージ・デザインについて、フラクタル次元及び主観のアンケートを実施しました。
(ブランドのバイアスを除くために地ビールを選定) - その結果、フラクタル次元の高いパッケージ・デザインを持った缶ビールに、高い購買効果がみられました。
The Relation of the Purchase Effect by the Fractal Dimension and the SD Method of Product Packaging:Oyama-Higa,
Mayumi, 59 ( 2 ) , pp.77 - 93 , 2012-12 , 近畿大学商経学会
被験者:23名(男:11名、女:12名)
実験内容:45種類の缶ビールのフラクタル次数を算出/缶ビールの購買効果のアンケートを実施

-
インターネットの報告によると、フラクタル次元の高い缶ビールでは、売り上げ実績、人気が高い傾向がみられました。
➊、➋:ビアコンテストで賞を獲得 ➌:地ビール売れ筋ランキング1位(楽天市場での報告より)
➍:人気ランキング1位(Yahooショッピングの報告より) - フラクタル次元の低い缶ビールは、売り上げ実績や人気が高い傾向はありませんでした。
ラベルのフラクタル次元が高い缶ビール群

ラベルのフラクタル次元が低い缶ビール群

